Gran hexecontaedro icosacrónico

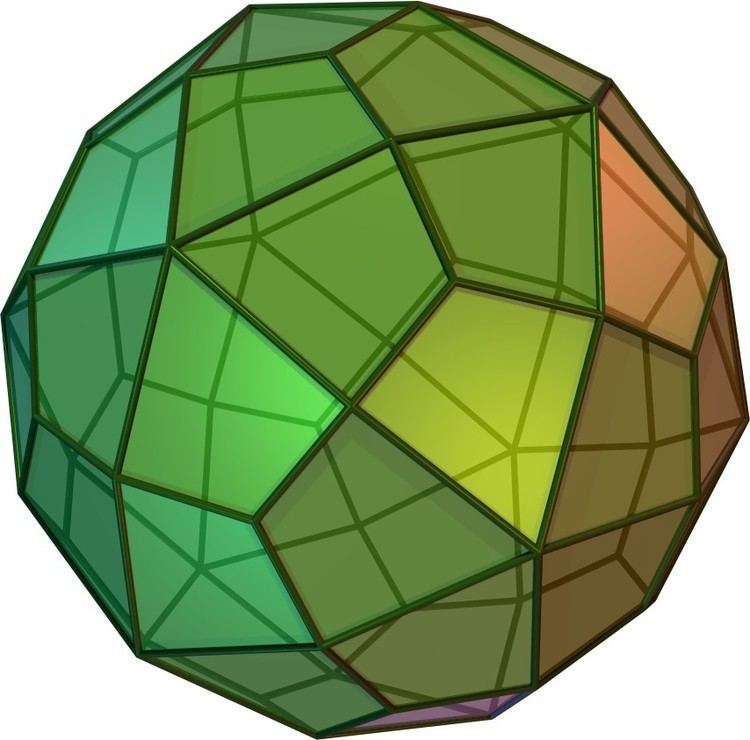
En geometría, el gran hexecontaedro icosacrónico (o gran trisicosaedro sagital) es el dual del gran icosicosidodecaedro.^[1]​ Sus caras son dardos. Una parte de cada dardo se encuentra dentro de la figura, por lo que no son totalmente visibles en los modelos sólidos.

Proporciones

Las caras tienen dos ángulos de ${\displaystyle \arccos({\frac {3}{4}} {\frac {1}{20}}{\sqrt {5}})\approx 30.480\,324\,565\,36^{\circ }}$, uno de ${\displaystyle \arccos(-{\frac {1}{12}} {\frac {19}{60}}{\sqrt {5}})\approx 51.335\,802\,942\,83^{\circ }}$ y otro de ${\displaystyle 360^{\circ }-\arccos(-{\frac {5}{12}} {\frac {1}{60}}{\sqrt {5}})\approx 247.703\,547\,926\,46^{\circ }}$. Su ángulo diedro es igual a ${\displaystyle \arccos({\frac {-44 3{\sqrt {5}}}{61}})\approx 127.686\,523\,427\,48^{\circ }}$. La relación entre las longitudes de los bordes largo y corto es ${\displaystyle {\frac {31 5{\sqrt {5}}}{22}}\approx 1.917\,288\,176\,70}$.

Referencias

Enlaces externos

• Weisstein, Eric W. «Great icosacronic hexecontahedron». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.