Coseno

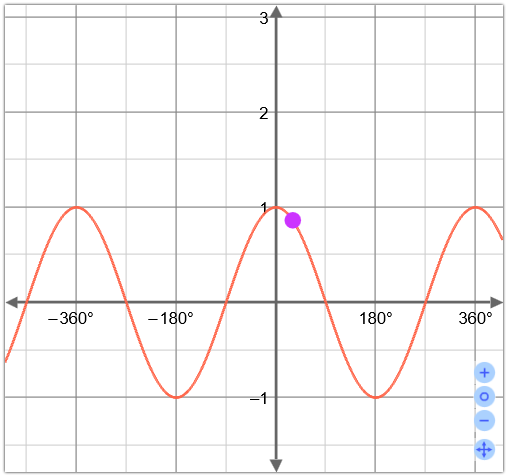
En matemáticas, el coseno es una función par y continua con periodo ${\displaystyle 2\pi }$, además una función trascendente. Su nombre se abrevia cos.

${\displaystyle \cos \;x=\cos(-x)}$

${\displaystyle \cos \;x=-\cos(x \pi )}$

En trigonometría, el coseno de un ángulo ${\displaystyle \alpha }$ de un triángulo rectángulo se define como la razón entre el cateto adyacente a dicho ángulo y la hipotenusa:

${\displaystyle \cos \alpha ={\frac {b}{c}}={\frac {AC}{AB}}}$

Esta razón no depende del tamaño del triángulo rectángulo escogido sino que es una función dependiente del ángulo ${\displaystyle \alpha .}$

Si ${\displaystyle B}$ pertenece a la circunferencia de radio uno con centro ${\displaystyle O=A}$ se tiene:

${\displaystyle \cos \alpha =b=AC}$

Ya que ${\displaystyle c=AB=1}$.

Esta construcción permite representar el valor del coseno para ángulos no agudos y funciona exactamente igual para los vectores, representando un vector ${\displaystyle {\vec {AB}}}$ mediante su descomposición en los vectores ortonormales ${\displaystyle {\vec {AC}}}$ y ${\displaystyle {\vec {CB}}}$.

Cálculo por serie de potencias

En análisis matemático el coseno es la función que asocia un número real ${\displaystyle x}$ con el valor del coseno del ángulo de amplitud, expresada en radianes, ${\displaystyle x}$. Es una función trascendente y analítica, cuya expresión en serie de potencias es:

${\displaystyle \cos x=1-{\cfrac {x^{2}}{2!}} {\cfrac {x^{4}}{4!}}-{\cfrac {x^{6}}{6!}} \ldots (-1)^{n}\;{\frac {x^{2n}}{(2n)!}} \ldots }$

que en sumatorio sería:

${\displaystyle \cos x=\sum _{n=0}^{\infty }\;(-1)^{n}\;{\frac {x^{2n}}{(2n)!}}}$

En el plano complejo

En el plano complejo a través de la fórmula de Euler se tiene que:

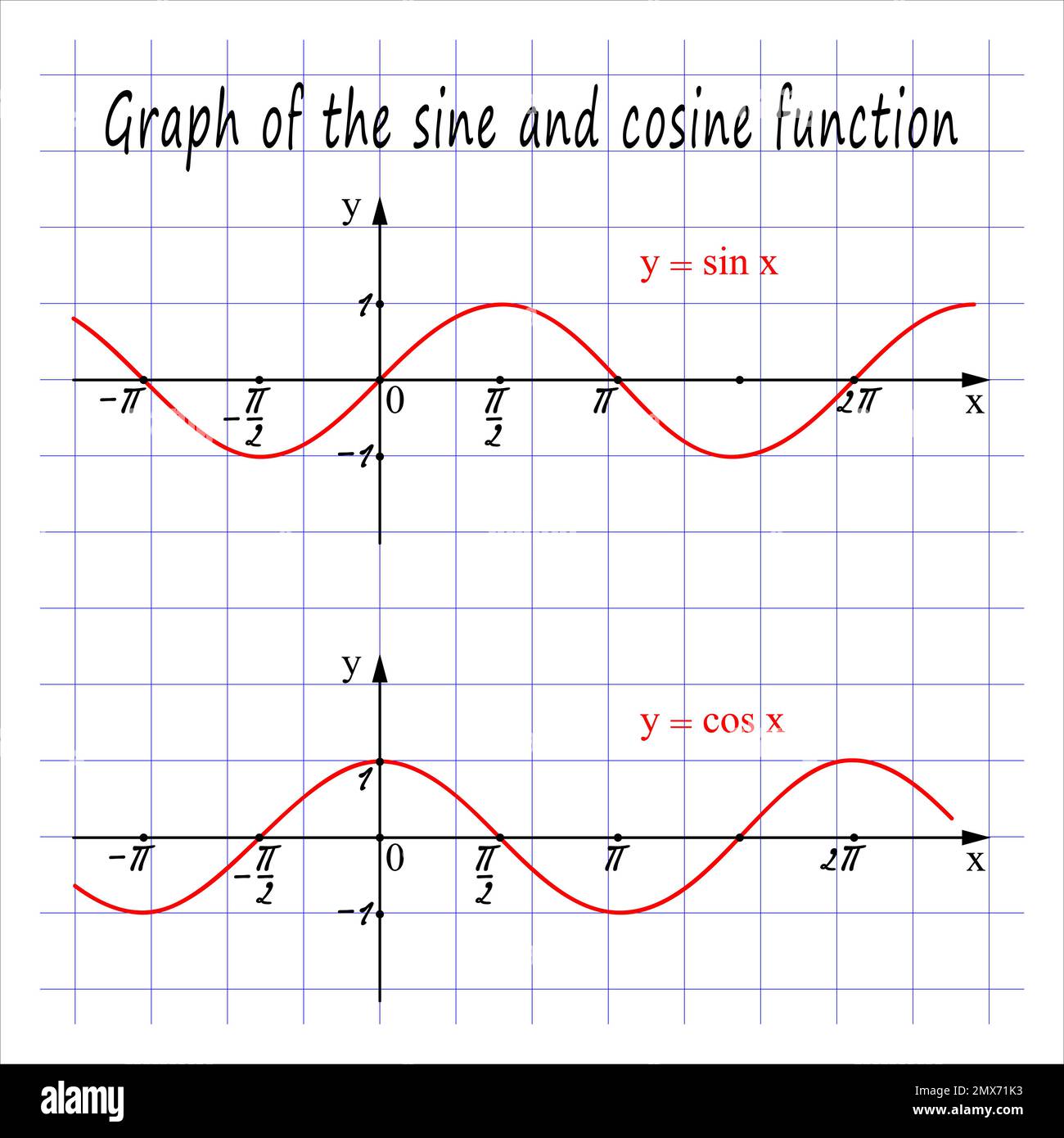
Representación gráfica

Relaciones trigonométricas

El coseno puede relacionarse con otras funciones trigonométricas mediante el uso de identidades trigonométricas.

Relación entre el seno y el coseno

La curva del coseno es la curva del seno desplazada ${\displaystyle {\frac {\pi }{2}}}$ a la izquierda dando lugar a la siguiente expresión:

${\displaystyle \cos \alpha =\operatorname {sen} \left(\alpha {\frac {\pi }{2}}\right)}$

Coseno de la suma de dos ángulos

Coseno del ángulo doble

Coseno del ángulo mitad

Suma de funciones como producto

Producto de funciones como suma

${\displaystyle \cos(A)\cos(B)=\cos ^{2}\left({\frac {A B}{2}}\right)-\;\operatorname {sen} ^{2}\left({\frac {A-B}{2}}\right)=\cos ^{2}\left({\frac {A-B}{2}}\right)-\;\operatorname {sen} ^{2}\left({\frac {A B}{2}}\right)}$

${\displaystyle \cos(A)\cos(B)={\frac {1}{2}}\left(\cos(A B) \cos(A-B)\right)}$

Ángulos para los cuales el coseno se conoce con exactitud

Tomando los mismos valores para los ángulos con signo opuesto a los ángulos enunciados en la tabla, puesto que el coseno es una función par.

Derivada del coseno

${\displaystyle \cos 'x=-\operatorname {sen} x\,}$

Generalizaciones del coseno

• Coseno hiperbólico cosh(x)
• Función elíptica cn(x)

Véase también

• Sinusoide
• Función
• Función par
• Trigonometría
• Funciones trigonométricas

Enlaces externos

• Weisstein, Eric W. «Coseno». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.